第一章 概论

1.2 对称密钥加密

对称密钥（秘密密钥）：双方共享密码信息（密钥）

• 消息本身称为明文
• 加密后的消息称为密文

对称密钥加密方案包含的三个算法：密钥产生、加密、解密

• 密钥产生算法（Gen）：概率算法，根据方案定义的某种分布选择并输出一个密钥k
• 加密算法（Enc）：输入密钥k和明文m，输出密文c。记为$Enc_k(m)$
• 解密算法（Dec）：输入密钥k和密文c，输出明文m。记为$Dec_k(c)$
• 密钥空间（K）：密钥产生函数输出的所有可能密钥称为密钥空间
• 明文（消息）空间（M）：所有被加密算法支持的消息的集合
• 一个加密方案可由明确三个算法（Gen，Enc，Dec）和明文空间M来完全定义

攻击场景

• 唯密文攻击：仅已知密文

• 已知明文攻击：已知一个或多个使用相同密钥加密的明文/密文对

• 选择明文攻击：可以选择明文得到其对应密文

• 选择密文攻击：可以选择密文得到其对应明文

1.3 古典加密术及其密码分析

凯撒加密：移位3字母

移位加密:密钥k∈(0,25)，加密时字母移动k个位置

密钥空间充分性原则：任何安全的加密方案必须拥有一个能够抵御穷举搜索的密钥空间

单字母替换（substitution）：一一映射

多字母移位加密（Vigenere）：如图

第二章 完善保密加密

2.1 完善保密加密

完善保密加密：

完美不可区分性：密文不包含任何明文信息（密文空间的概率分布独立于明文？）

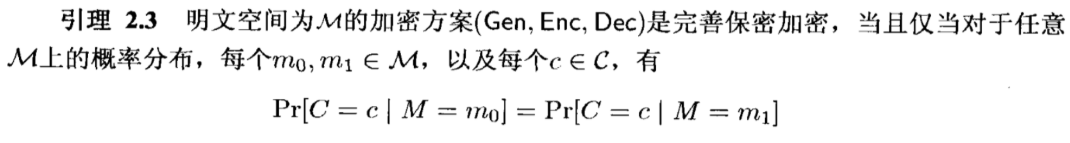
敌手不可区分性：敌手不能区分密文时来自哪个明文的加密

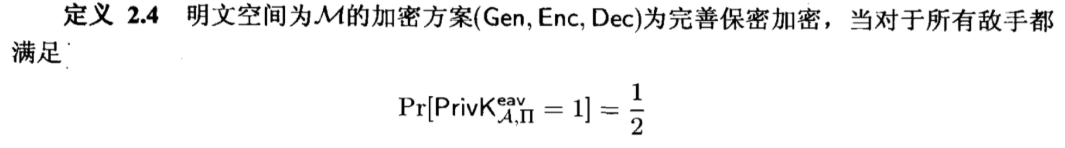
其中：

2.2 一次一密（Vernam加密）

2.3 完善保密加密局限

2.4 香农定理

定理：设加密方案 （Gen,Enc,Dec）的明文空间为M，且|K|=|M|=|C|，则当且仅当下列条件成立时，此方案是完善保密加密：

• 由Gen产生的任意密钥k∈K的概率都是1/|K|。
• 对任意明文m∈M和任意密文c∈C，只存在唯一的密钥k∈K使得$Enc_k(m)$输出c。

$$a+b=c$$

---