第三章 对称密钥加密及为随机性

3.1密码学的计算方法

信息理论安全与计算安全

• 信息理论安全：完善保密加密
• 计算安全：使用具体方法和渐进方法来定义：
  • 具体方法：如果每个运行时间最多为$t$的敌手以最多为$\varepsilon$的概率成功公婆该方案，则称这个方案为$(t,\varepsilon)$安全
  • 渐进方法：如果每个PPT（多项式时间）敌手以可忽略的概率成功攻破一个方案，那么该方案是安全的
    • 注：在任何加密方案中，密钥空间必须足够大，以至于敌手不能变量，或者说，密钥空间的时间规模必须为安全参数的超多项式

有效的算法与可忽略的成功概率

• 有效计算：指能够在“概率多项式时间”（PPT）内执行的计算
• 可忽略的成功概率：如果对于每一个多项式$p(.)$，存在一个$N$，使得所有的整数$n>N$，都满足$f(n)<1/p(n)$，则函数$f$是可忽略的

如何证明某个密码构造是安全的

1. 指定PPT敌手$A$攻击，并将成功的概率表示为$\varepsilon(n)$
2. 构造一个叫做”规约“的有效算法$A~’$（区分器？）,该算法将敌手$A$作为子程序来使用，试图解决难题$X$。
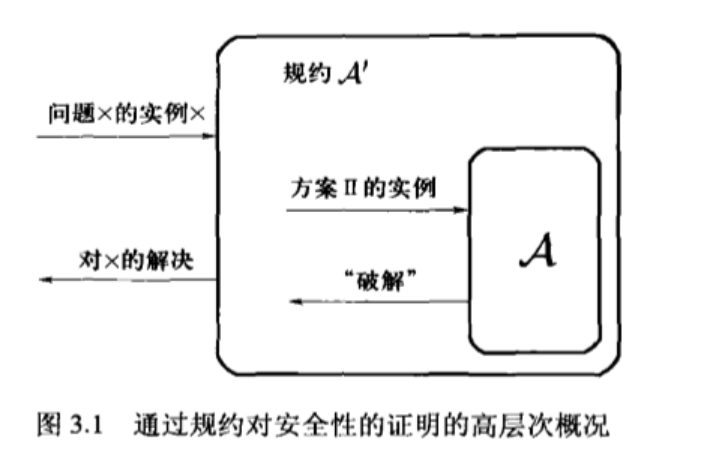
3. 如果能成功攻破，那么说明该区分器可以区分这个加密算法所使用的伪随机生成器
4. 但是根据伪随机生成器的定义，不可被区分
5. 所以矛盾，证明该算法安全

3.2 定义计算安全的加密

窃听者存在情况下的不可区分性

​ 窃听者不可区分实验$PrivK^{eav}_{A,\Pi}(n)$:

• 给定输入$1^n$给敌手$A$，$A$输出一对长度相等的消息$m_0$,$m_1$。
• 运行$Gen(1^n)$生成以个密钥k，选择一个随机比特$b$，$b∈\{0,1\}$。计算出密文$c=Enc_k(m_b)$，并且给$A$。把$c$叫做挑战密文。
• $A$输出一个比特$b’$
• 如果$b=b’$输出1，反之输出0.

定义：如果对于所有的概率多项式事件敌手$A$,存在一个可忽略函数$negl$使得：$Pr[PrivK^{eav}_{A,\Pi}<= 1/2 +negl(n)$,则一个对称密钥加密方案$\Pi=(Gen,Enc,Dec)$具备在窃听者存在的情况下不可区分的加密。

等价公式：$|Pr[output(PrivK^{eav}_{A,\Pi}(n,0))=1]-Pr[output(PrivK^{eav}_{A,\Pi}(n,1))=1]| <= negl(n)$