第五章 伪随机置换（分组加密）的实际构建

密码学第三次作业所需内容，密码学好难qaq，不想写作业。。。

5.1 代替——置换网络

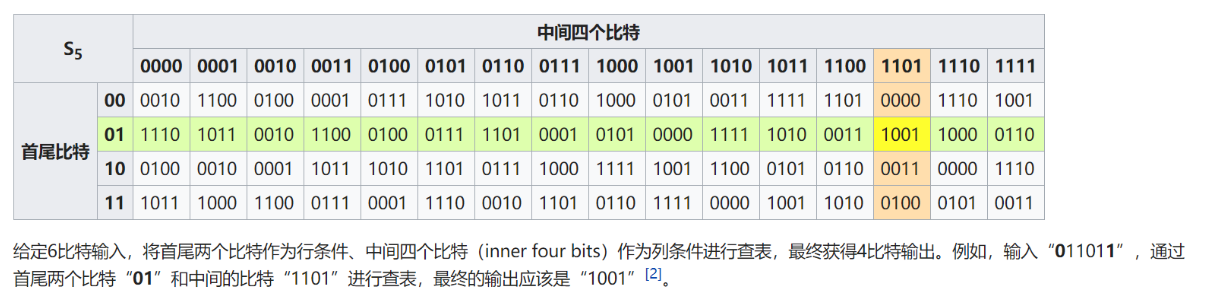
S盒（替换盒）：对称密钥加密算法执行替换计算的基本结构。在块密码中，通常被用于模糊密钥与密文之间的关系（香农的混淆理论）

通常，S-Box接受特定数量的输入比特$m$，并将其转换为特定数量的输出比特$n$，其中$n$不一定等于$m$。一个$m*n$的S-Box可以通过包含$2^m$条目，每条目$n$比特的查找表实现。DES和AES的S盒是固定的，也有一些加密算法的S盒是基于密钥动态生成的，比如Blowfish和双鱼算法。

P盒（置换盒）： 是一个透过置换和转置[替换盒（S-boxes）输入进行位元洗牌的方法，在转置的过程中保持一定程度的扩散。

置换盒通常分为三类：

• 压缩性的——输出位元数比输入少
• 扩张性的——输出位元数比输入多
• 平直性的——输出位元数等于输入位元数

其中只有平直性的置换盒是可逆的。

代替置换网络（SP）：

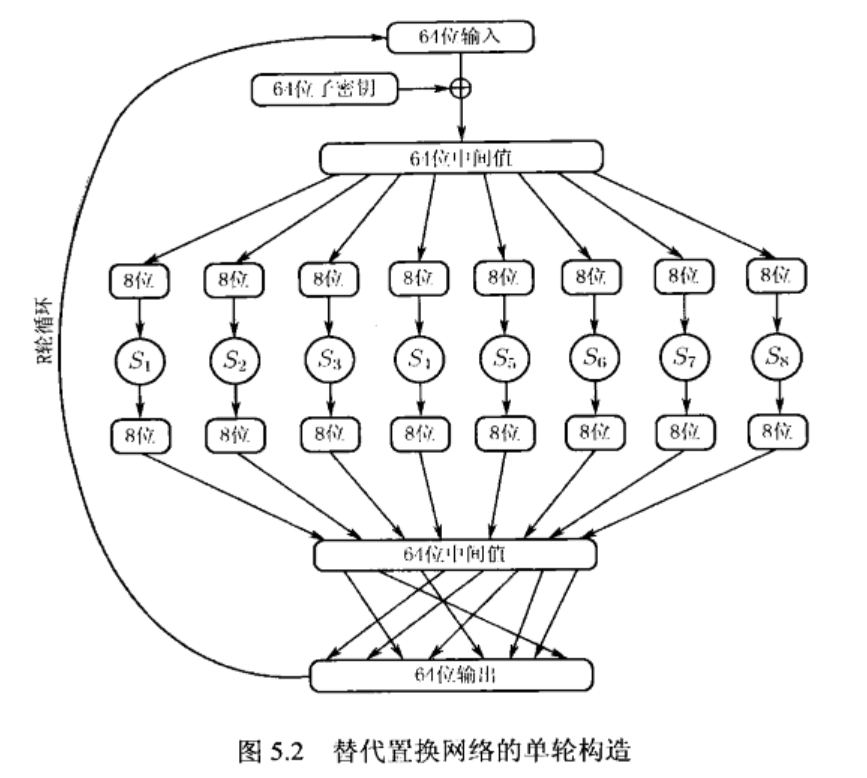
设计原则：

• S盒的可逆性：在代替置换网络中，S盒必须是可逆的（即必须是单射和满射函数），否则分组函数不能成为一个置换
• 雪崩效应：任何分组密码的一个重要特性就是输入的微小改变必然会导致输出的巨大改变，否则两个相似输入所生成的分组密码看起来就不是独立的了。因此，输入的单个比特的变化会影响每一个比特。
  • S盒的设计要使得改变S盒输入的单个比特就能改变S盒输出的至少两个比特
  • 混合置换的设计要使得任何给定的S盒的输出比特都被传递到下一轮中不同的S盒中

代替置换网络的安全性：

对轮数较少的代替转换网络的攻击：

攻击三轮代替-置换网络：

5.2 Feistel网络

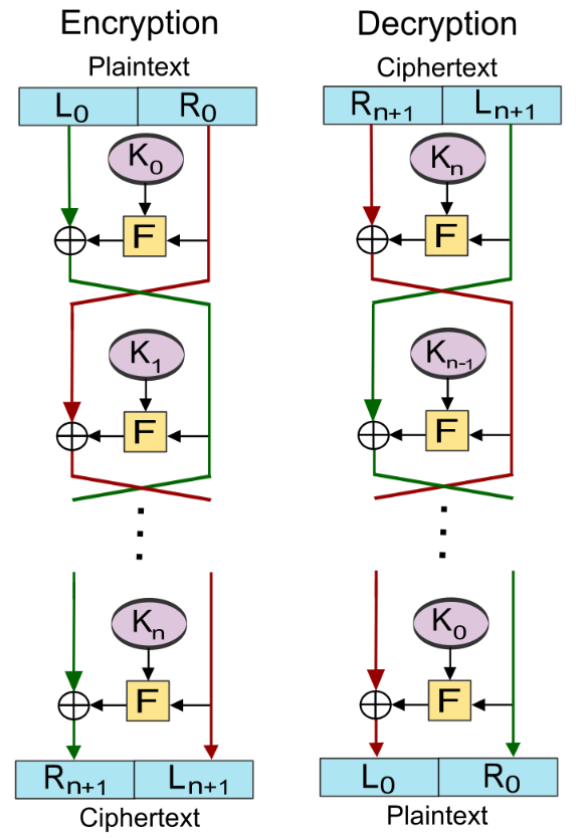
5.3 DES——数据加密标准

5.4 增加分组密码的密钥长度

5.5 AES——高级加密标准

5.6 差分密码盒线性密码分析简介

第六章 伪随机对象的理论构造

6.1 单向函数

单向函数的定义：

• 令$f:\{0,1\}^\rightarrow\{0,1\}^$为一个函数，$A$为任意算法，$n$为任意安全参数值：
  • 求逆实验$Invert_{A.f}(n)$
    • 选择输入$x\leftarrow\{0,1\}^n$，计算$y:=f(x)$
    • $1^n$和$y$值作为$A$的输入，输出为$x’$
    • 如果$f(x’)=y$，那么定义该实验输出为1，否则为0
• 定义：如果一个函数$f:\{0,1\}^\rightarrow\{0,1\}^$满足以下两个条件，那么它是单向函数：
  • （易于计算）存在多项式时间算法$M_f$来计算$f$,即对于所有的$x$，有$M_f(x)$
  • （反向求逆十分困难）对任意概率多项式时间算法$A$，存在一个可忽略函数$negl$，满足：$Pr[Invert_{A,f}(n)=1]\leqslant negl(n)$
    • 也可表示为：$Pr_{x\leftarrow\{0,1\}^n}[A(f(x))∈f^{-1}(f(x))] \leqslant negl(n) $

单向置换：