​ 数据库系统6——查询处理&查询优化。

查询处理

关系代数操作算法

选择操作算法

• 简单选择操作算法：
  • 线性搜索算法
    • 顺序读取被操作关系的每个元组
    • 测试该元组是否满足条件，满足则输出
  • 二元搜索算法
    • 条件：按该属性排序
    • $O(log(N))$
  • 主索引或者HASH搜索
    • 条件：主索引属性或者HASH属性上的相等比较
  • 使用主索引查找满足条件的元组
    • 条件：主索引属性上的非相等比较
  • 使用聚集索引查找满足条件的元组
    • 具有聚集索引的非键属性上的相等比较
  • B+树和B树索引搜索算法
  • 合取选择算法
  • 使用复合索引的合取选择算法

投影操作算法

• 若投影结果中包含码：存取R的所有元组一次即可完成
• 若不包含：需要删除重复元组。可利用排序算法实现投影操作
• 

连接操作算法

$\theta-$连接操作算法：

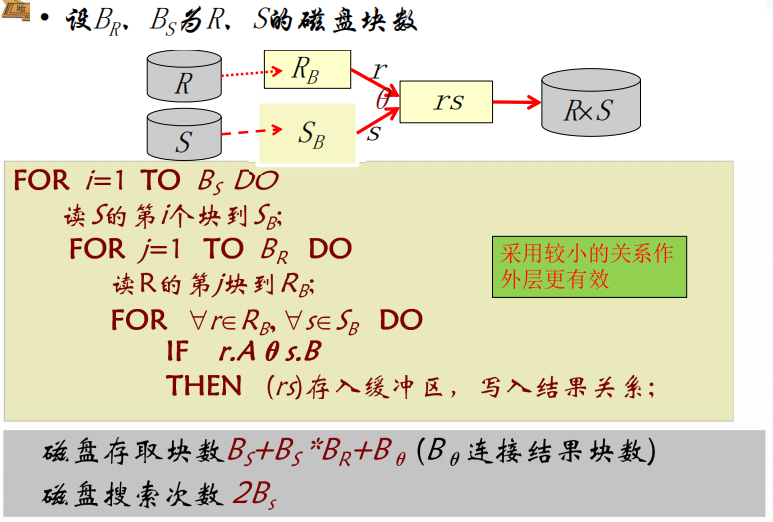
等值连接操作算法：（这里讨论自然连接）

• 循环嵌套链接（NLJ）

  

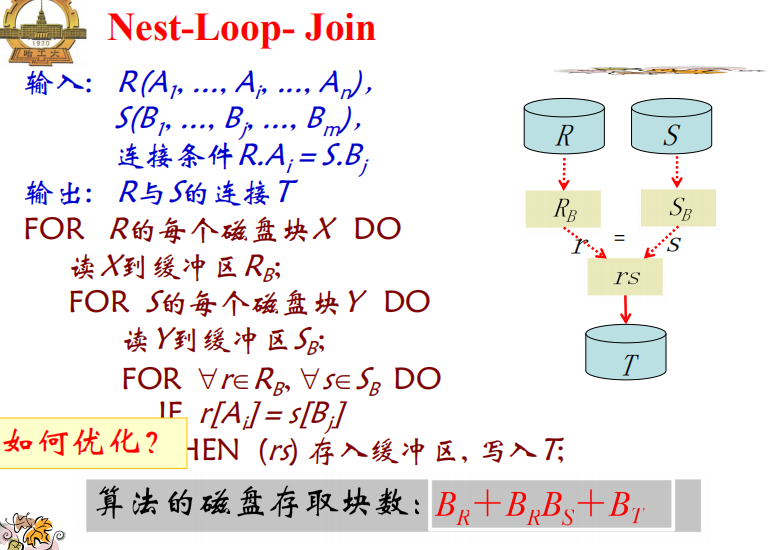
  • 优化：一次读入尽可能多的元组；使用尽可能多的内存块存放外层循环关系的元组；较小的作为外层。

• 排序合并连接（Sort-Merge-Join）

  ​

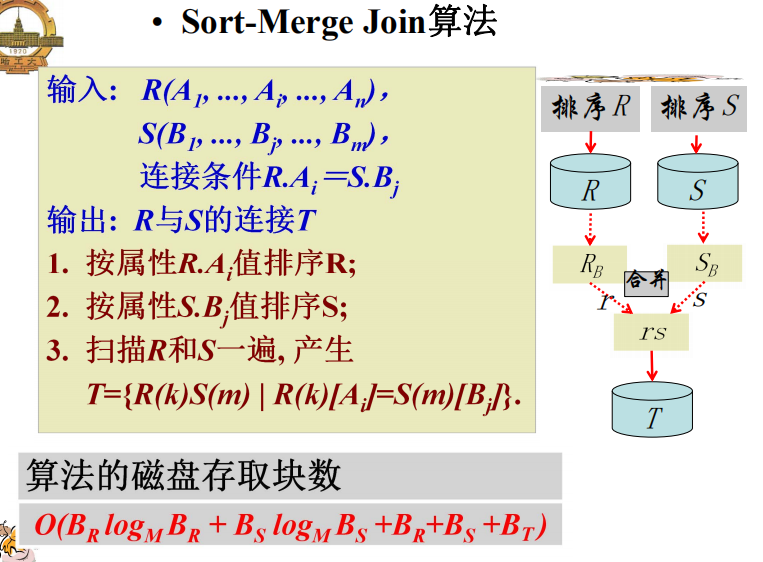
• Hash-连接（Hash-Join）

  ​

集合操作算法

输入关系约束：具有相同的属性集合且属性的排列顺序也相同

方法：利用排序算法在相同的键属性上排序两个操作关系，然后扫描排序后的关系，完成集合操作。

本章重点：掌握个操作的实现算法；掌握关系代数表达式的查询处理方法

查询优化

使用不同的策略处理查询会得到不同的时间开销，需要选择优化的查询处理策略，以减少处理时间，提高系统的处理能力。

关系表达式的等价转换规则

关系代数等价转换规则：

• 选择串接率
  • $\sigma_{c1 and…and cn }(E) \equiv \sigma_{c1}(\sigma_{c2}(…(\sigma_{cn}(E))))$
• 选择交换律
  • $\sigma_{c1}(\sigma_{c2}(E)) \equiv \sigma_{c2}(\sigma_{c1}(E))$
• 投影交换律
  • $\Pi_{L1}(\Pi_{L2}(…(\Pi_{Ln}(E))…)) \equiv \Pi_{L1}(E)$
• 选择投影交换律
  • $\Pi_{L}(\sigma_C(E)) \equiv \sigma_C(\Pi_{L}(E)) $ —— C中只涉及L中属性
  • $\Pi_{L}(\sigma_C(E)) \equiv \Pi_{L}(\sigma_C(\Pi_{L,B1,B2,…,Bm}(E)))$ ——还涉及其他属性
• 连接和笛卡尔积的交换律
• 集合操作的交换律
• 连接、笛卡尔积和集合操作的结合律
• 选择、连接和笛卡尔乘积的分配律
• 投影、连接和笛卡尔乘积的分配律
• 选择与集合操作的分配律
• 投影与集合操作的分配律
• 其他

表达式结果大小的估计

一个操作的代价依赖于它的输入大小和其他统计信息

• 数据库系统的统计信息

  • $n_r$：关系r的元组数
  • $b_r$：包含关系r中元组的磁盘块数
  • $l_r$：关系r中每个元组的字节数
  • $f_r$：关系r的块因子（一个磁盘块中可以容纳r中元组的个数）
  • $V(A,r)$：关系r中属性A中出现的非重复值的个数

• 如果假设关系r在物理上存储于一个文件中，则 $b_r = \lceil n_r/ f_r\rceil$

• 当r中A属性上的取值分布是均匀的，运算结果的大小估计如下：

  • 投影$\Pi_A(r)$ ：$V(A,r)$

  • 选择$\sigma_{A=a}(R)$： $n_r/V(A,r)$

  • $\sigma_{A \leq v}(R)$：

    • $if v < min(A,r)$：0
    • $if v > max(A,r)：n_r$
    • else：$n_r \times [v-min(A,r)]/[max[A,r]-min(A,r)]$

  • 合取$\sigma_{\theta_1 \wedge…\wedge \theta_k}(R)$： $n_r \times分别的选择估计结果相乘/ n_r^k$

  • 析取：$(1-(1-计算结果_1/n_r)\times……)\times n_r$

  • 取反$\sigma_{\urcorner\theta}(r)$：无空值——$n_r-s_\theta$

    ​ 右空值——$n_r-n_{null}-s_\theta$

  • 笛卡尔积：元素个数之积，每个元组占$l_r+l_s$个字节

  • 自然连接：RS交集为空：类似笛卡尔积的结果

    ​ RS交集为R的码：小于等于$n_s$

    ​ 交集为S中参照R的外码：$n_s$

    ​ 不是任何的码：$min(n_r\times n_s/V(A,s),n_s\times n_r/V(A,r))$

  • 聚集：$V(A,r)$

  • 集合运算：类似于合取、析取、取反的估计方法

  • 外连接（结果上界）：

    • r左外连接s：自然连接估值+$n_r$
    • r右外连接s：自然连接估值+$n_s$
    • r全外连接s：自然连接估值+$(n_r+n_s)$

• 当r中A属性上的取值分布不均匀的，可以采用直方图等统计方法统计方法进行结果大小估计。

启发式关系代数优化算法

• 启发式代数优化规则

  给定一个关系代数表达式，可以应用一组启发式规则对其进行等价变换，产生一个具有较高效率的等价表达式。（不能保证一定产生最优化等价表达式）

  • 选择和投影操作尽早执行

  • 把某些选择操作与笛卡尔积相结合，形成一个连接操作

  • 同时执行相同关系上的多个选择和投影操作
  • 把投影操作与连接操作结合起来执行
  • 提取公共表达式（如果一个反复出现的公共表达式结果不是很大，且从外存读入的时间小于计算时间，可以组织计算一次并存储结果）

• 启发式代数优化算法

  • 构造查询的内部表示是查询处理的第一步。给定一个用高级语言定义的查询，需要两步来构造该查询的内部表示。
    • 把高级语言定义的查询转换为关系代数表达式
      • 使用from从句中的关系构造笛卡尔积，然后再这个基础上构造选择操作，最后构造投影操作
    • 把关系代数表达式转化为查询树
  • 算法流程：
    • 把每个选择操作$\sigma_{C1 and….and Cn}(E)$转化为$\sigma_{C1}(…(\sigma_{Cn}(E))…)$
    • 把每个选择操作移到尽可能靠近叶结点
    • 把每个投影操作尽可能靠近叶结点
    • 把串接的多个选择或多个投影操作组合为单个的选择或投影操作
    • 重新安排叶结点，使既有最小选择操作的叶结点最先执行
    • 组合笛卡尔积和相继的选择操作形成连接操作
    • 把最后的查询树划分为多个子树，使得每个子树上的操作可以由单个存取程序一次完成，划分方法如下：
      • 每个耳目操作在且仅在一个子树中
      • 如果二目操作a在子树t中，而且从叶到根的方向的路径b$\rightarrow$a是仅包含一目操作的最长路径，则b$\rightarrow$a也包含在t中
    • 产生一个计算最后查询树的程序，每一步计算一个子树

基于复杂性估计的查询优化算法

两个阶段：

• 用启发式优化算法产生逻辑上优化的关系代数表达式或查询计划p
• 为p中每个关系代数操作选择具有最小复杂性的实现算法，确定p的优化执行策略p(A)
• 影响查询执行效率的主要因素是磁盘存取块数

本章重点：熟练掌握关系代数表达式等价变换规则；掌握启发式查询优化算法。